Graph

1. Overview

A Graph consists of a finite set of vertices(or nodes) and a set of edges that connect a pair of nodes.

2. Description

2.1 Components

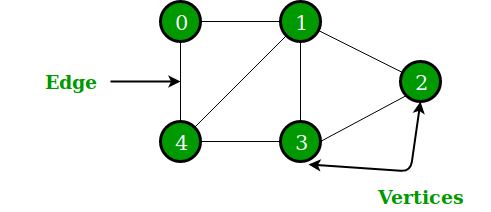
2.1.1 Edge

In the above Graph, the set of edges E = {(0,1), (1,2), (2,3), (3,4), (0,4), (1,4), (1,3)}.

2.1.2 Vertice

In the above Graph, the set of vertices V = {0,1,2,3,4}

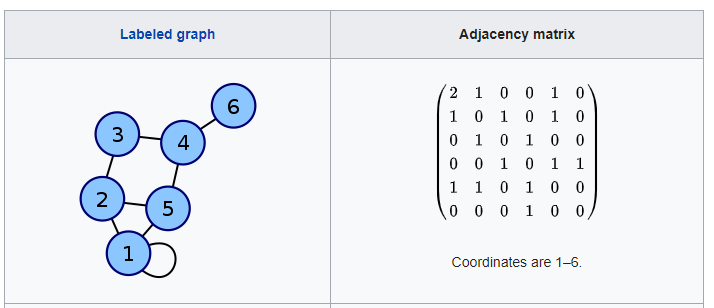
2.1.3 Adjacency matrix

Represents graph with 'V' nodes into a VxV 0-1 matrix where $A_{ij} = 1$ means that vertex 'i' and 'j' are connected.

class Graph(object):
    def __init__(self, size):
        self.adjMatrix = []
        for i in range(size):
            self.adjMatrix.append([0 for i in range(size)])
        self.size = size
    def addEdge(self, v1, v2):
        if v1 == v2:
            print("Same vertex %d and %d" % (v1, v2))
        self.adjMatrix[v1][v2] = 1
        self.adjMatrix[v2][v1] = 1
    def removeEdge(self, v1, v2):
        if self.adjMatrix[v1][v2] == 0:
            print("No edge between %d and %d" % (v1, v2))
            return
        self.adjMatrix[v1][v2] = 0
        self.adjMatrix[v2][v1] = 0
    def containsEdge(self, v1, v2):
        return True if self.adjMatrix[v1][v2] > 0 else False
    def __len__(self):
        return self.size
        
    def toString(self):
        for row in self.adjMatrix:
            for val in row:
                print('{:4}'.format(val)),
            print
        
def main():
        g = Graph(5)
        g.addEdge(0, 1);
        g.addEdge(0, 2);
        g.addEdge(1, 2);
        g.addEdge(2, 0);
        g.addEdge(2, 3);
    
        g.toString()
            
if __name__ == '__main__':
   main()

• Pros:
  • Easy to implement
  • Removing an edge takes O(1) time
  • Queries like whether there is an edge from vertex 'u' to vertex 'v' are efficient and can be done O(1)
• Cons:
  • Consumes more space O($V^{2}$)
  • Adding a vertex is O($V^{2}$) time

2.1.4 Adjacency List

An array of linked lists is used. The size of the array is equal to the number of vertices and each entry of array corresponds to a linked list of vertices adjacent to this index.

graph = {'A': set(['B', 'C']),
         'B': set(['A', 'D', 'E']),
         'C': set(['A', 'F']),
         'D': set(['B']),
         'E': set(['B', 'F']),
         'F': set(['C', 'E'])}

• Pros:
  • Saves space $O(\left | V \right |+\left | E \right |)$, worst case $O(V^{2})$
  • Adding a vertex is easier
• Cons:
  • Queries like whether there is an edge from vertex u to vertex v are not efficient and can be done O(V)

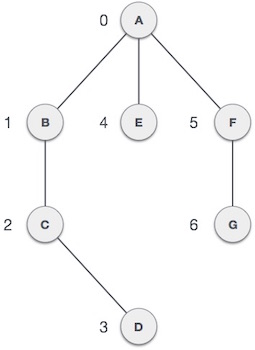
2.1.6 Path

The path represents a sequence of edges between the two vertices. In the following example, ABCD represents a path from A to D

2.2 Time and Space Complexity

	Adjacency list	Adjacency matrix	Incidence matrix
Store graph	$O(\left | V \right |+\left | E \right |)$	$O(\left | V \right |^{2})$	$O(\left | V \right |\cdot \left | E \right |)$
Add vertex	O(1)	$O(\left | V \right |^{2})$	$O(\left | V \right |\cdot \left | E \right |)$
Add edge	O(1)	O(1)	$O(\left | V \right |\cdot \left | E \right |)$
Remove vertex	$O(\left | E \right |)$	$O(\left | V \right |^{2})$	$O(\left | V \right |\cdot \left | E \right |)$
Remove edge	$O(\left | V \right |)$	O(1)	$O(\left | V \right |\cdot \left | E \right |)$
Are vertices x and y adjacent (assuming that their storage positions are known)?	$O(\left | V \right |)$	O(1)	$O(\left | E \right |)$
Remarks	Slow to remove vertices and edges, because it needs to find all vertices or edges	Slow to add or remove vertices, because matrix must be resized/copied	Slow to add or remove vertices and edges, because matrix must be resized/copied

2.3 Traversal

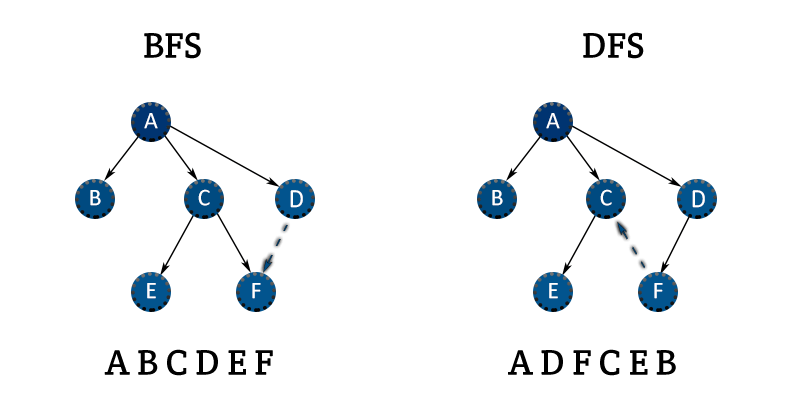
• BFS visits all of the neighbours before visiting children nodes. DFS visits all children nodes before visiting neighbours.
• For implementation, BFS uses a queue data structure, while DFS uses a stack.
• BFS uses a larger amount of memory because it expands all children of a vertex and keeps them in memory. It stores the pointers to a level’s child nodes while searching each level to remember where it should go when it reaches a leaf node. DFS has much lower memory requirements than BFS because it iteratively expands only one child until it cannot proceed anymore and backtracks thereafter. It has to remember a single path with unexplored nodes.
• Both have the same O(n) time complexity, but BFS is “better” at finding the shortest path in a graph, while DFS is “better” at answering connectivity queries (determining if every pair of vertices can be connected by two disjoint paths).

2.3.1 Breadth First Traversal (BFT)

import collections
def bfs(graph, root): 
    visited, queue = set(), collections.deque([root])
    visited.add(root)
    while queue: 
        vertex = queue.popleft()
        for neighbour in graph[vertex]: 
            if neighbour not in visited: 
                visited.add(neighbour) 
                queue.append(neighbour) 
if __name__ == '__main__':
    graph = {0: [1, 2], 1: [2], 2: [3], 3: [1,2]} 
    breadth_first_search(graph, 0)

Application:

• Check if a graph is connected
• Generating spanning tree
• Finding the shortest path in a graph

2.3.2 Depth First Traversal (DFT)

# Using a Python dictionary to act as an adjacency list
graph = {
    'A' : ['B','C'],
    'B' : ['D', 'E'],
    'C' : ['F'],
    'D' : [],
    'E' : ['F'],
    'F' : []
}

visited = [] # Array to keep track of visited nodes.

def dfs(visited, graph, node):
    if node not in visited:
        print node,
        visited.append(node)
        for neighbour in graph[node]:
            dfs(visited, graph, neighbour)

# Driver Code
dfs(visited, graph, 'A')

Application:

• Testing connectivity
• Finding a path between two nodes
• Solving puzzles

2.4 Types of Graphs

2.3.1 Undirected Graph

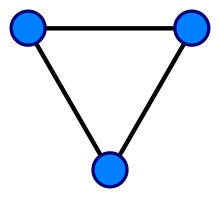
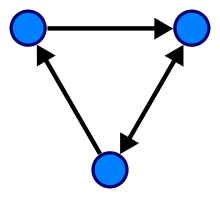
2.3.2 Directed Graph

A directed graph or digraph is a graph in which edges have orientations.

3. References

https://en.wikipedia.org/wiki/Graph_(abstract_data_type)

https://en.wikipedia.org/wiki/Adjacency_matrix

https://www.tutorialspoint.com/data_structures_algorithms/graph_data_structure.htm

https://www.geeksforgeeks.org/graph-data-structure-and-algorithms/#introDFSnBFS

https://www.geeksforgeeks.org/dijkstras-algorithm-for-adjacency-list-representation-greedy-algo-8/

https://www.youtube.com/watch?v=zaBhtODEL0w

https://www.youtube.com/watch?v=1n5XPFcvxds&feature=emb_title

https://www.youtube.com/watch?v=Y40bRyPQQr0

https://www.youtube.com/watch?v=0u78hx-66Xk

https://www.programiz.com/dsa/graph-adjacency-matrix

https://www.programiz.com/dsa/graph-adjacency-list

https://eddmann.com/posts/depth-first-search-and-breadth-first-search-in-python/

https://www.educative.io/edpresso/how-to-implement-depth-first-search-in-python

https://open4tech.com/bfs-vs-dfs/