Clustering analysis

1. Overview

Cluster analysis or clustering is the task of grouping a set of objects in such a way that objects in the same group (called a cluster) are more similar (in some sense) to each other than to those in other groups (clusters). It is the main task of exploratory data mining, and a common technique for statistical data analysis, used in many fields, including machine learning, pattern recognition, image analysis, information retrieval, bioinformatics, data compression, and computer graphics.

2. Definition

Let given sample data set $\boldsymbol{X}=\left \{ \boldsymbol{x_{1},x_{2},\cdots ,x_{N}} \right \}$

where $\boldsymbol{x_{i}}$ is ith sample of $d$ dimension feature vector $\boldsymbol{x_{i}} =(\boldsymbol{x_{i1},x_{i2},\cdots ,x_{id}})^{T} $

 

Find clustering solution $C=\left \{ c_{1},c_{2},\cdots ,c_{k} \right \}$ 

where commonly $k\ll  N$

2.1 Hard clustering

$$\left.\begin{matrix}
c_{i}\neq \varnothing ,\, i=1,\cdots ,k  \\ 
\cup _{i=1,k}\, c_{i}=\mathbf{X}\\ 
c_{i}\cap c_{j}=\varnothing ,\, i\neq j
\end{matrix}\right\}$$

 

2.2 Soft clustering

$$\left.\begin{matrix}
0\leq m_{ij}\leq 1  \\ 
\sum_{j=1}^{k}m_{ij}=1\\ 
\sum_{j=1}^{N}m_{ij}< N
\end{matrix}\right\}$$

 

where $m_{ij}$ is degree of $x_{i}$ classified into $c_{j}$

 

2.3 Stirling

The number of ways to partition a set of N objects into k non-empty subsets. It can be defined as recurrence relation as below:

 

$$\left.\begin{matrix}
S(N,k)=S(N-1,k-1)+kS(N-1,k)\\ 
S(N,1)=1\\ 
S(N,N)=1
\end{matrix}\right\}$$

 

where $S(n,k)=\frac{1}{k!}\sum_{i=0}^{k}(-1)^{i}\binom{k}{i}(k-i)^{n}$

 

Dynamic programming of Stirling recurrence relation

3. Distance and Similarity

3.1 Categories of Data

3.1.1 Quantitative

3.1.2 Qualitative

• Ordinal
• Nominal

3.2 Distance and Similarity

3.2.1 Minkowski distance

$$d_{ij}=\left ( \sum_{k=1}^{d}\left | x_{ik}-x_{jk} \right |^{p} \right )^{\frac{1}{p}}$$

• Euclidean distance

$$d_{ij}=\sqrt{\sum_{k=1}^{d}(x_{ik}-x_{jk})^{2}}$$

where $p=2$

• Manhattan distance

$$d_{ij}=\sum_{k=1}^{d}\left | x_{ik}-x_{jk} \right |$$

where $p=1$

• Mahalanobis distance

$$D_{M}(\vec{x})=\sqrt{(\vec{x}-\vec{\mu })^{T}S^{-1}(\vec{x}-\vec{\mu })}$$

• Hamming distance

the minimum number of substitutions required to change one string into the other, or the minimum number of errors that could have transformed one string into the other

3.2.2 Similarity

$$s_{ij}=d_{max}-d_{ij}$$

 

• cosine similarity

$$s_{ij}=cos\, \theta =\frac{x_{i}^{T}x_{j}}{\left \| x_{i} \right \|\left \| x_{j} \right \|}$$

where $s_{ij}\subset \left [ 0,1 \right ]$

 

$$s_{ij}=\frac{n_{00}+n_{11}}{n_{00}+n_{11}+n_{01}+n_{10}}$$

 

where $n_{00}$ is number of two feature all two feature are 0, and so on

 

$$s_{ij}=\frac{n_{11}}{n_{11}+n_{01}+n_{10}}$$

 

where $n_{00}$ is not considerable

 

Convert similarity to distance when $s_{max}$ is maximum:

$$d_{ij}=s_{max}-s_{ij}$$

 

3.2.3 Distance between feature and cluster

$$D_{max}(\boldsymbol{x_{i}},c_{j})=\underset{\boldsymbol{y_{k}}\in c_{j}}{max}\, d_{ik}$$

$$D_{min}(\boldsymbol{x_{i}},c_{j})=\underset{\boldsymbol{y_{k}}\in c_{j}}{min}\, d_{ik}$$

$$D_{ave}(\boldsymbol{x_{i}},c_{j})=\frac{1}{\left | c_{j} \right |}\sum_{\boldsymbol{y_{k}}\in c_{j}}d_{ik}$$

 

where $\left | c_{j} \right |$ is size of sample and sample $\boldsymbol{y_{k}}$ is classified to cluster $c_{j}$ and $d_{ik}$ denote distance between $\boldsymbol{x_{i}}$ and $\boldsymbol{y_{k}}$

 

and distance between sample and representative of cluster is also optional like below:

 

$$\left.\begin{matrix}
D_{mean}(\boldsymbol{x_{i}},c_{j})=d_{i,mean}\\ 
\boldsymbol{y_{mean}}=\frac{1}{\left | c_{j} \right |}\sum_{\boldsymbol{y_{k}}\in c_{j}}\boldsymbol{y_{k}}
\end{matrix}\right\}$$

 

where $\boldsymbol{y_{k}}$ is representative of $c_{j}$ and $d_{i,mean}$ is distance of $\boldsymbol{x_{i}}$ and $\boldsymbol{y_{mean}}$

 

more general expression like below:

 

$$\left.\begin{matrix} 
D_{rep}(\boldsymbol{x_{i}},c_{j})=d_{i,rep}\\  
\sum_{\boldsymbol{y_{k}}\in c_{j}}\, d_{rep,k}\leq \sum_{\boldsymbol{y_{k}}\in c_{j}}\, d_{l,k},\, \forall \boldsymbol{y_{l}}\in c_{j}
\end{matrix}\right\}$$

3.2.3 Distance between two cluster

$$D_{max}(c_{i},c_{j})=\underset{\boldsymbol{x_{k}}\in c_{i},\boldsymbol{y_{l}}\in c_{j}}{max}\, d_{kl}$$

$$D_{min}(c_{i},c_{j})=\underset{\boldsymbol{x_{k}}\in c_{i},\boldsymbol{y_{l}}\in c_{j}}{min}\, d_{kl}$$

$$D_{ave}(c_{i},c_{j})=\frac{1}{\left | c_{i} \right |\left | c_{j} \right |}\sum_{\boldsymbol{x_{k}}\in c_{i}}\sum_{\boldsymbol{y_{l}}\in c_{j}}d_{kl}$$

$$D_{mean}(c_{i},c_{j})=d_{mean1,mean2}$$

where $\boldsymbol{x_{mean1}}=\frac{1}{\left | c_{i} \right |}\sum_{\boldsymbol{x_{k}}\in c_{i}}\boldsymbol{x_{k}},\, \boldsymbol{y_{mean2}}=\frac{1}{\left | c_{j} \right |}\sum_{\boldsymbol{y_{l}}\in c_{j}}\boldsymbol{y_{l}}$

 

more general form of representative distance is like below:

$$D_{rep}(c_{i},c_{j})=d_{rep1,rep2}$$

where $$\sum_{\boldsymbol{x_{k}}\in c_{i}}\, d_{rep1,k}\leq \sum_{\boldsymbol{x_{k}}\in c_{i}}\, d_{p,k},\, \forall \boldsymbol{x_{p}}\in c_{i},\,\sum_{\boldsymbol{y_{l}}\in c_{j}}\, d_{rep2,l}\leq \sum_{\boldsymbol{y_{l}}\in c_{j}}\, d_{p,l},\, \forall \boldsymbol{y_{p}}\in c_{j}$$

 

3.2.4 Dynamic distance

• Levenshtein distance
• Damerau-Levenshtein distance

4. Classification of clustering algorithms

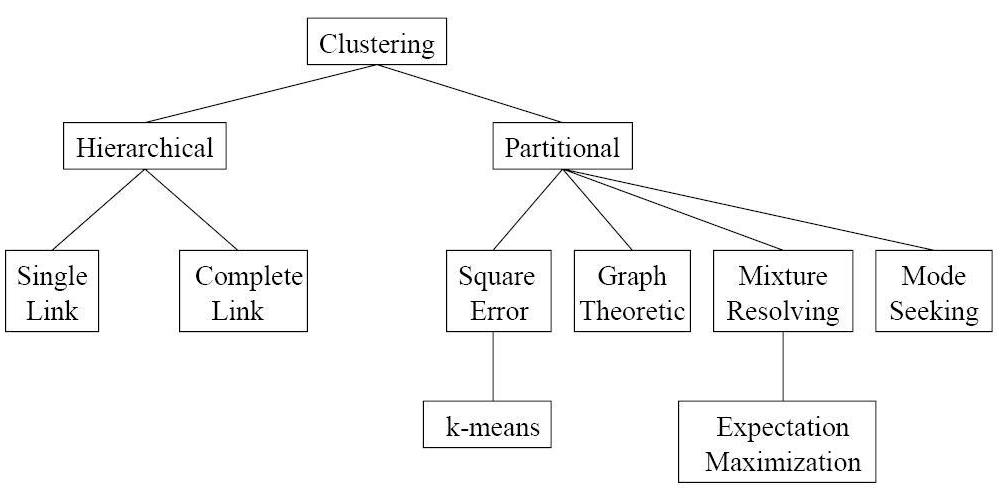
5. Hierarchical clustering

5.1 Agglomerative

bottom-top approach

outlier sensitive

5.2 divisive

top-down approach

Binary Space Partitioning complexity $S(n,2)=2^{n-1}-1$

5.3 dendrogram

6. Partitional clustering

6.1 Sequential algorithm

time complexity $O(k_{max}N)$

where commonly $k_{max} \ll N$, so $k_{max}$ can be treated as constant. So can be reduced like below:

$$O(N)$$

6.2 k-means algorithm

6.3 model-based 

7. References

https://en.wikipedia.org/wiki/Cluster_analysis

https://en.wikipedia.org/wiki/Stirling_numbers_of_the_second_kind

https://stats.stackexchange.com/questions/159902/is-nominal-ordinal-binary-for-quantitative-data-qualitative-data-or-both

https://en.wikipedia.org/wiki/Hamming_distance

https://en.wikipedia.org/wiki/Mahalanobis_distance#targetText=The%20Mahalanobis%20distance%20is%20a,from%20the%20mean%20of%20D.

https://en.wikipedia.org/wiki/Cosine_similarity

https://grid.cs.gsu.edu/~wkim/index_files/SurveyParallelClustering.html

http://www.mit.edu/~9.54/fall14/slides/Class13.pdf