Projections in RN space

1. Overview

A projection is a linear transformation P from a vector space to itself such that$P^{2}=P$. That is, whenever P is applied twice to any value, it gives the same result as if it were applied once (idempotent). It leaves its image unchanged. Though abstract, this definition of "projection" formalizes and generalizes the idea of graphical projection. One can also consider the effect of a projection on a geometrical object by examining the effect of the projection on points in the object.

2. Projections in $R^{2}$

2.1 Notation

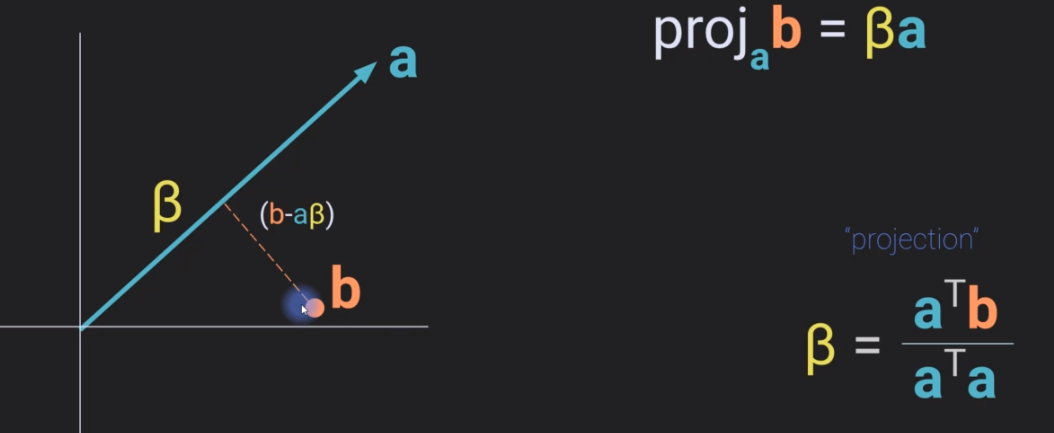
2.2 Procedure

3. Projection in $R^{N}$

3.1 Procedure

3.2 Equation Intuition

So what we're saying with this equation is that vector D is in the column space of matrix C and the elements in vector x tell us the weightings the coefficients the ways to combine the columns of C that will give us vector D.

How do you know how to weigh the columns such that the weighted combination of the columns of C gives us vector D? The answer is, of course, to solve for x by inverting C and putting it on the left the right-hand side of the equation left multiplying vector D.

3.3 If A is a square full-rank matrix:

If that's the case then we can apply the inverse to each of these matrices individually swapping the order of course because of the live evil rule. So that gives us An inverse over here and then An inverse transpose on the right.

3. Reference

https://en.wikipedia.org/wiki/Projection_(linear_algebra)

https://en.wikipedia.org/wiki/Projection_matrix