Binary Search Tree

1. Overview

Unlike other sequential structures such as linked list, queue, stack, and array, which are one element after another and sort of a line of things, It has a hierarchical data structure like a tree. A tree whose elements have at most 2 children is called a binary tree. Since each element in a binary tree can have only 2 children, we typically name them the left and right child.

• Root: The topmost node is called the root of the tree
• Leaf: elements with no children are called leaves
• Parent: The element directly above something
• Children: The elements that are directly under an element 
• Depth: The length of the (unique) path from the root down to that node
• Height: The length of the longest path from that node to a leaf below it

2. Description

2.1 Properties

2.1.1 The maximum number of nodes at level 'I' of a binary tree is $2^{I-1}$

2.1.2 Maximum number of nodes in a binary tree of height 'h' is $2^{h}-1$

2.1.3 In a Binary Tree with N nodes, minimum possible height or minimum number of levels is $log_{2}(N+1)$

2.1.4 A Binary Tree with L leaves has at least $log_{2}L + 1$ levels

2.1.5 In Binary tree where every node has 0 or 2 children, the number of leaf nodes is always one more than nodes with two children.

2.2 Adding Node

To add an element so we can find it later, it has to be added along the search path that will be used. To add an element, we first search for it. If found, it need not be added; if not found, it is added as a child of the leaf node reached along the search path. Again, this can be written easily as a tail-recursive method

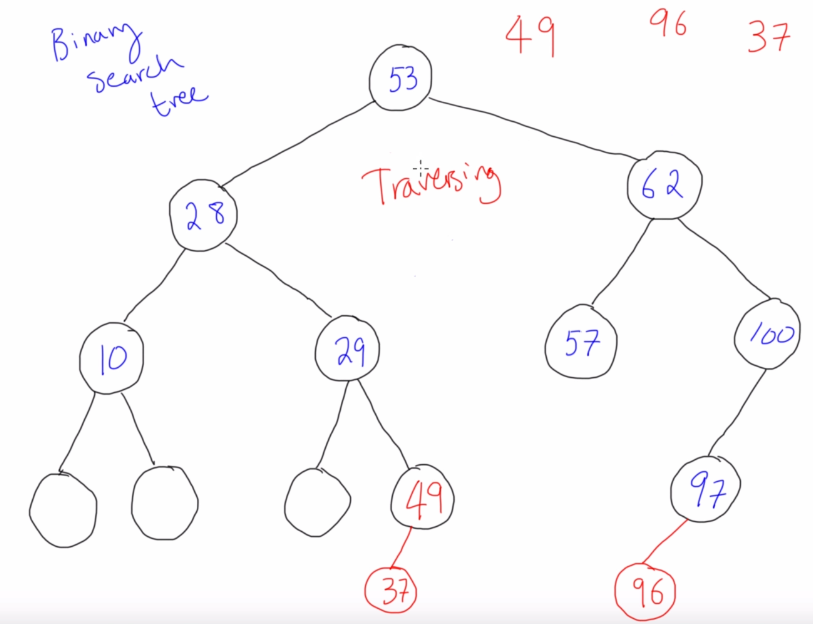
To see how this algorithm works, consider adding the element 49. We start at the root (53) and go to the left (28) because 49 < 53. In the recursive call, we then go to the right (28 < 49) to node 29. Since 29 < 49, we try to go to the right but observe right == null, and therefore create a right child containing 49. 

2.3 Deleting Node

2.3.1 Simple deleting

If we delete node 7 which has no children. All we have to do is changing the reference the right child of 5 to point to None. So in Java or Python, the garbage collection framework comes in and just cleans it up for us. In other programming languages such as C++, you actually have to go and wipe this node out in memory if not it will be a dangling pointer.

2.3.2 Deleting a node has a children

If we delete 71 node, all we would have to do is the right child of 52 is going to be reassigned to 63. So effectively what we're doing is taking subtree which was a child of 71 and just plugging it into 71's position

2.3.3 Deleting a node has two children

If we delete 25 node, what do we do? Use inorder search to find a successor. we have to find a number of a node within this binary search tree that can safely take the place of 25. The way to determine that is we need to find the smallest of the set of nodes that are larger than the original node which was 25.

2.2 Traversal 

For each node n in the tree, all data stored in n's left subtree are less than the data stored at n, and all data stored in n's right subtree are greater than the data stored at n.

Depth First Traversals:
(a) Inorder (Left, Root, Right) : 4 2 5 1 3
(b) Preorder (Root, Left, Right) : 1 2 4 5 3
(c) Postorder (Left, Right, Root) : 4 5 2 3 1

Breadth-First or Level Order Traversal: 1 2 3 4 5

2.2.1 Inorder Traversal

Algorithm Inorder(tree)
   1. Traverse the left subtree, i.e., call Inorder(left-subtree)
   2. Visit the root.
   3. Traverse the right subtree, i.e., call Inorder(right-subtree)

2.2.2 Preorder Traversal

Algorithm Preorder(tree)
   1. Visit the root.
   2. Traverse the left subtree, i.e., call Preorder(left-subtree)
   3. Traverse the right subtree, i.e., call Preorder(right-subtree) 

2.2.3 Postorder Traversal

Algorithm Postorder(tree)
   1. Traverse the left subtree, i.e., call Postorder(left-subtree)
   2. Traverse the right subtree, i.e., call Postorder(right-subtree)
   3. Visit the root.

2.3 Time and Space Complexity

Algorithm	Average	Worst
Space	O(n)	O(n)
Search	O(log n)	O(n)
Insert	O(log n)	O(n)
Delete	O(log n)	O(n)

2.3 Type of binary tree

2.3.1 Full Binary Tree

A full binary tree (sometimes proper binary tree or 2-tree) is a tree in which every node other than the leaves has two children

2.3.2 Complete Binary Tree

A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible

2.3.3 Perfect Binary Tree

2.3.4 Balanced Binary Tree

All internal nodes have exactly two children and all leaf nodes are on the same level

2.3.5 Degenerate (or pathological) tree

A Tree where every internal node has one child. Such trees are performance-wise same as linked list.

3. Difference between Binary Tree and Binary Search Tree

A binary tree is a nonlinear data structure where each node can have at most 2 child nodes.

Now, if I ask you to search any node in the above tree what will you do? well, you will search the entire tree until you get the desired node. so, In worst-case complexity for searching a node is O(n).

Binary search tree is a binary tree in which a node has a value greater than all values in its left subtree and smaller than all values in its right subtree.

4. Reference

https://en.wikipedia.org/wiki/Binary_tree

https://www.geeksforgeeks.org/binary-tree-data-structure/

https://emre.me/data-structures/binary-tree/

https://www.geeksforgeeks.org/tree-traversals-inorder-preorder-and-postorder/

https://www.youtube.com/watch?v=cO6RsSmSjio&feature=emb_title

https://www.cs.cornell.edu/courses/cs2112/2018fa/lectures/lecture.html?id=trees

\https://www.quora.com/What-is-the-difference-between-a-binary-tree-and-a-binary-search-tree