Linear Algebra Features

1. Overview

Summarize Terminologies and features

2. Description

2.1 Matrix multiplications

It doesn't matter if you're multiplying $A^{T}A$ or $AA^{T}$ both results will produce not only a Square matrix but a Symmetric matrix.

2.1.1 Characteristic equation

The characteristic equation is the equation that is solved to find a matrix's eigenvalues, also called the characteristic polynomial. For a general n by n matrix A, the characteristic equation in variable $\lambda$ is defined by

$$\left | A-\lambda I \right |=0$$

2.1.2 Transpose Symmetric matrix

$$A^{T}=A$$

2.1.3 Power of Diagonal matrix

2.2 Vector space

A vector space (also called a linear space) is a collection of objects called vectors, which may be added together and multiplied ("scaled") by numbers, called scalars

2.2 Matrix Rank

the rank of a matrix A is the dimension of the vector space generated (or spanned) by its columns

C($AA^{T}$)=C(A)

R($AA^{T}$)=R(A)

2.2 Diagonal Matrix

$A^{T}A=A^{2}$ when A is a diagonal matrix.

invertible, full rank, and reduced rank.

nontrivial null space

2.2 Matrix Inverse

A singular matrix is a square matrix that is not invertible. Alternatively, a matrix is singular if and only if it has a determinant of 0. When an $nxn$ matrix is taken to represent a linear transformation in n-dimensional Euclidean space, it is singular if and only if it maps any n-dimensional hypervolume to an n-dimensional hypervolume of zero volume.

2.2.1 inverse of a diagonal matrix

2.2 Matrix Space

2.2.1 difference between subset and subspace

all matrices have four subspaces: the column space the row space the null space and the left null space. And if not satisfied this condition, it's a subset. Below equation is a subset because it doesn't include 0.

2.2.1 Nullspace

the null space of a matrix is the set of all vectors that you can multiply by a matrix to make this equation true. Where this zero, this is a bolded zero, so this is the zero vector, excluding the case the trivial case where the vector is simply the zeros vector itself.

It's an entire subspace and you can pick one vector. In this example, I'm picking the vector one minus one to be used as a basis for the null space of this matrix.

2.2.2 Relation to independence

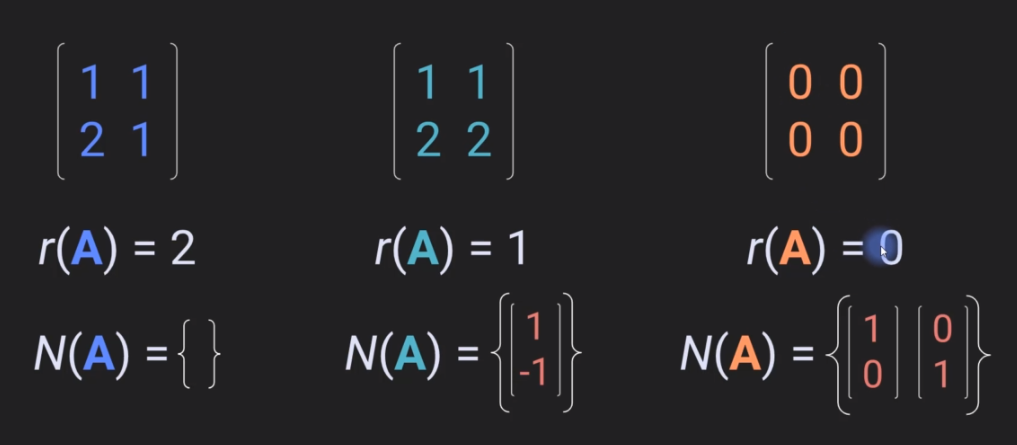
2.2.3 Left null space of a matrix

• It's the same idea the same concept but now it's a row vector that's on the left side of the matrix.
• And then, of course, the resulting 0 vector is also a row vector
• left null space is actually the regular null space of the matrix transpose.

2.2.2 Trivial null space

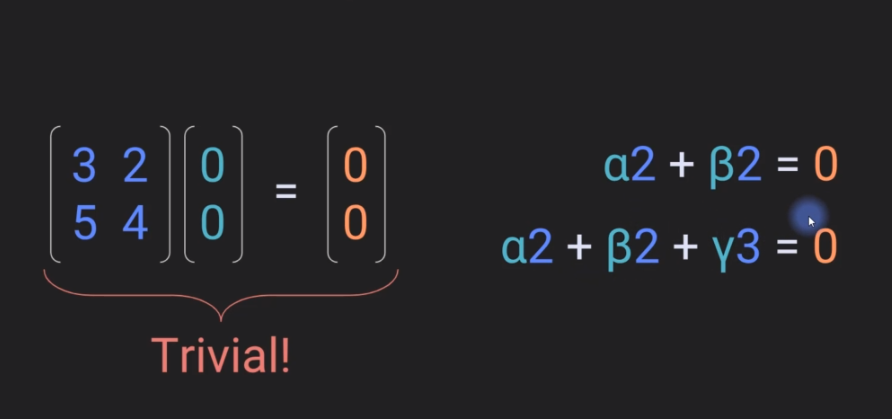
Matrix times some coefficients vector produces the zero vector. Only the trivial case's matrix does not have a null space or the null space is empty.

2.2.3 Nontrivial null space

Some vector of coefficients V1 and V2 such that the linear weighted combination of the columns in this matrix gives us the zero vector without the vector coefficients themselves all being equal to zero. In this case, this matrix has null space

2.2 Orthogonal Matrix

All orthogonal matrices have singular values of 1's

$AA^{T}=I$ when A is an orthogonal matrix

$A^{T}=A^{-1}$ when A is an orthogonal matrix

2.2 Eigendecomposition

The eigendecomposition of a symmetric positive semidefinite (PSD) matrix yields an orthogonal basis of eigenvectors, each of which has a nonnegative eigenvalue

2.3 SVD

Singular vector of A

singular value non-negative, but can be zero

3. Reference

https://math.stackexchange.com/questions/768098/what-kind-of-matrix-is-it-that-when-multiplied-with-its-transpose-produces-the-i

https://www.youtube.com/watch?v=hOn9QUcgnG4

https://en.wikipedia.org/wiki/Singular_matrix