Item-Item Collaborative Filtering

Intuition

• The correlation between the column vectors is high
• If you like Power Rangers, you'll also like Transformers because users give them similar ratings

	Power Rangers	Transformers	Ninja Turtles
User 1	4.5	5	4
User 2	5	5	4.5
User 3	1	2	0.5
User 4	2	2	0.5

User-User Collaborative Filtering

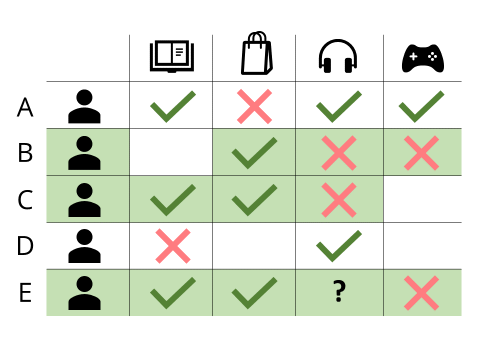
• For user-user CF, I want to find "users like me"
• The movies that those users have seen, that I haven't seen, become my recommendations
• It's intuitive that if they are "like me", I would like movies they've rated highly
• Looks row-wise
• Each row is a vector
• 2 users are similar in their row vectors have a small distance between them

Item-Item Collaborative Filtering

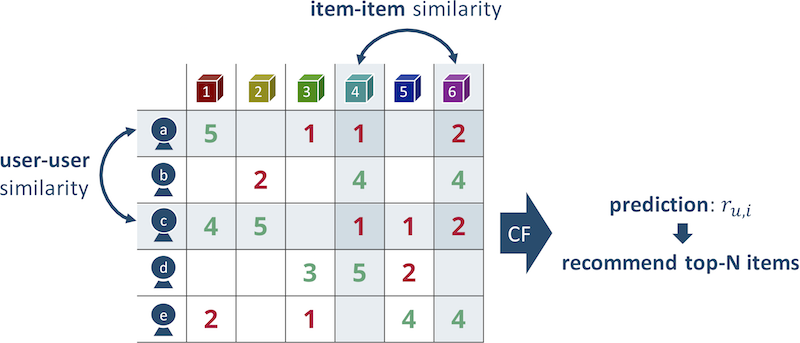
• What if we looked column-wise instead?
• Let's find 2 products that are similar
• They are similar if their column vectors' distance is small

Item Correlation

$$w_{ii'}=\frac{\sum_{j\in\Omega_{ii'}}(r_{ij}-\bar{r}_{i})(r_{i'j}-\bar{r}_{i'})}{\sqrt{\sum_{j\in\Omega_{ii'}}(r_{ij}-\bar{r}_{i})^2}\sqrt{\sum_{j\in\Omega_{ii'}}(r_{i'j}-\bar{r}_{i'})^2}}$$

$\Omega_{j}=users \ who \ rated \ item \ j$

$\Omega_{jj'}=users \ who \ rated \ item \ j \ and \ item \ j'$

$\bar{r}_{j}=average \ rating \ for \ item \ j$

Item Score

$$s(i,j)=\bar{r}_{i}+\frac{\sum_{i'\in\Psi_{j}}{w_{ii'}(r(i',j)-\bar{r}_{i'})}}{\sum_{i'\in\Psi_{j}}|w_{ii'}|}$$

$\Psi= items \ user \ i \ has \ rated$

• Deviation: how much user i likes item j', compared to how much everyone else likes j' (IMO, not as intuitive as user-user CF)
• If user i really likes j' (more than other users do) and j is similar to j' ($w_{jj'}$ is high), then user i probably likes j too

Comparison

• User-User CF: choose items for a user, because those items have been liked by similar users
• Item-Item CF: choose items for a user, because this user has liked similar items in the past
• By flipping the ratings matrix sideways, we can convert user-user CF algorithm into an item-item CF algorithm
• User-based and Item-based CF are mathematically identical
• Item-based CF is more accurate because more data to work with

Practical differences

• When comparing 2 items, you have a lot more data than when comparing 2 users
  • Each user: up to ~ 20k items to look at
  • Each item: up to 100k users to look at
  • Thus for item-based CF, weights are calculated based on more data
• Item-based CF is faster
  • Given a user, calculate scores for each item: $O(M^{2}N)
    • There are $M^{2}$ item-item weights, and each vector is length N
  • For user-based CF we saw $O(N^{2}M)$
  • N >> M, so $N^{2}$ compared to $M^{2}$ is even worse
• Item-based CF is more accurate

Limitation

• Item-based CF may be too accurate
• It's always suggesting similar products
• This leads to a lack of diversity in recommendations - the YouTube problem
• Worse MSE might be more desirable

The Cold-Start Problem

• We know that if we don't have enough data, we can't calculate correlations
• What if we don't have any data at all?
  • Add a prior to the average
  • The score can be a weighted sum of prediction + prior average
  • No data at all -> rely solely on prior
  • How to get prior? Scrape from the web or something else

Not necessarily movies/ratings

• user-item matrix doesn't have to be ratings at all
• Explicit feedback is sparse
• # of times user viewed a product
• Did they purchase?
• Hit like?
• Share on social media?

Reference

https://www.cs.umd.edu/~samir/498/Amazon-Recommendations.pdf

https://takuti.github.io/Recommendation.jl/latest/collaborative_filtering/

https://docs.aws.amazon.com/personalize/latest/dg/native-recipe-sims.html