Linear independence

1. Overview

2. Description

2.1 Definition

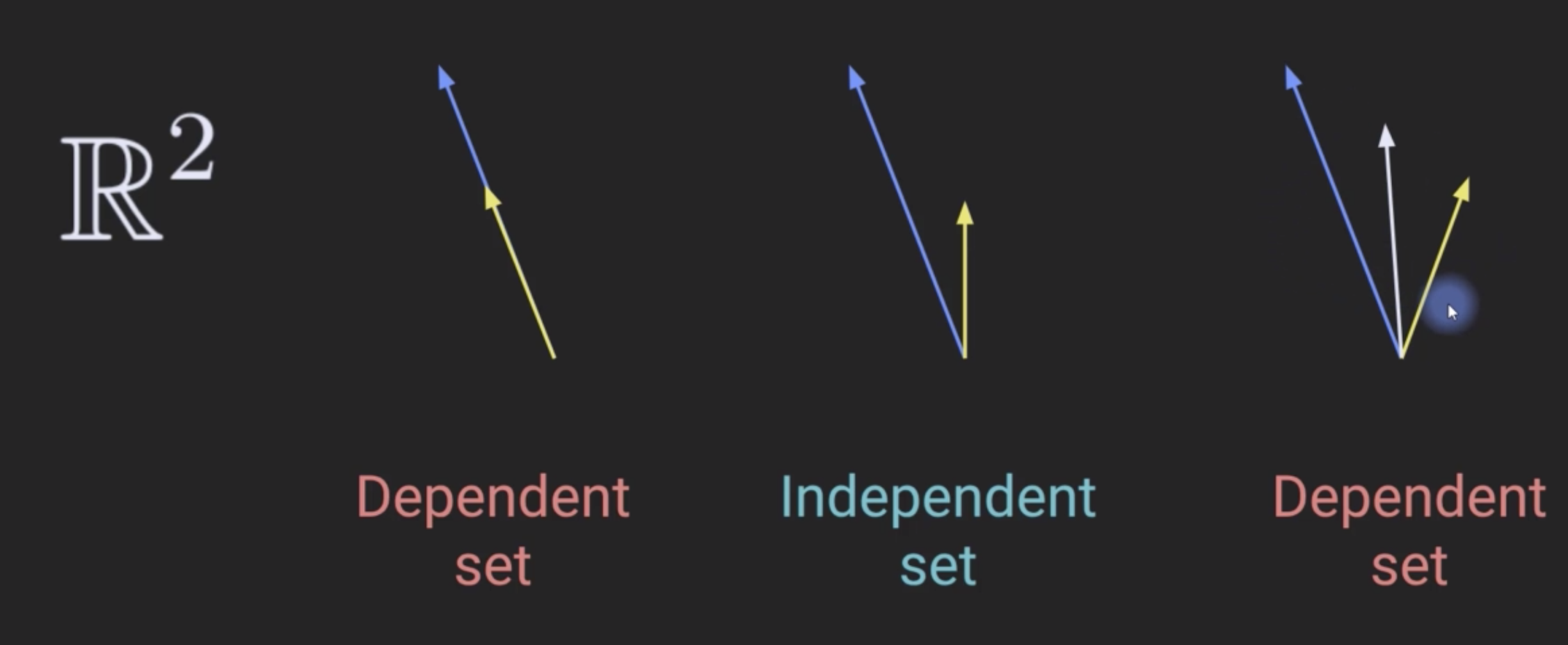
A set of M vectors is independent if each vector points in a geometric dimension not reachable using other vectors in the set.

Any set of M>N vectors in $\mathbb{R}^{N}$ is dependent

Any set of $M\leq N$ vectors in $\mathbb{R}^{N}$ could be independent

2.2 How to determine whether a set is independent

Step 1: Count vectors and compare with $R^{N}$

Step 2: Check for 0's in corresponding (or all) elements

Step 3: Educated guess and test

Step 4: Matrix rank method

3. Example

3.1 Dependent set

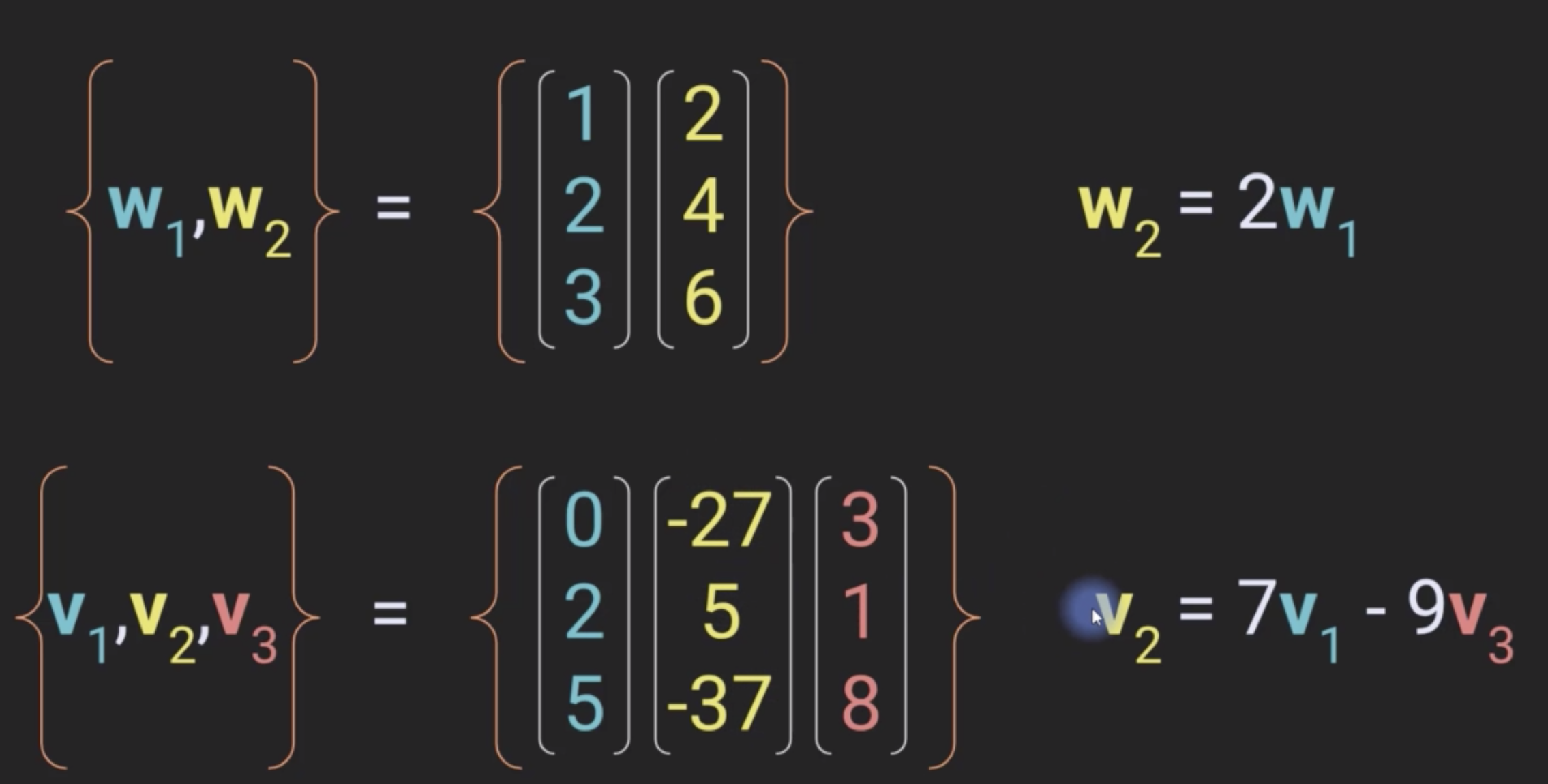
3.2 Independent set

4. References

https://en.wikipedia.org/wiki/Linear_independence