Combinatorics

1. Overview

2. Description

2.1 Permutation

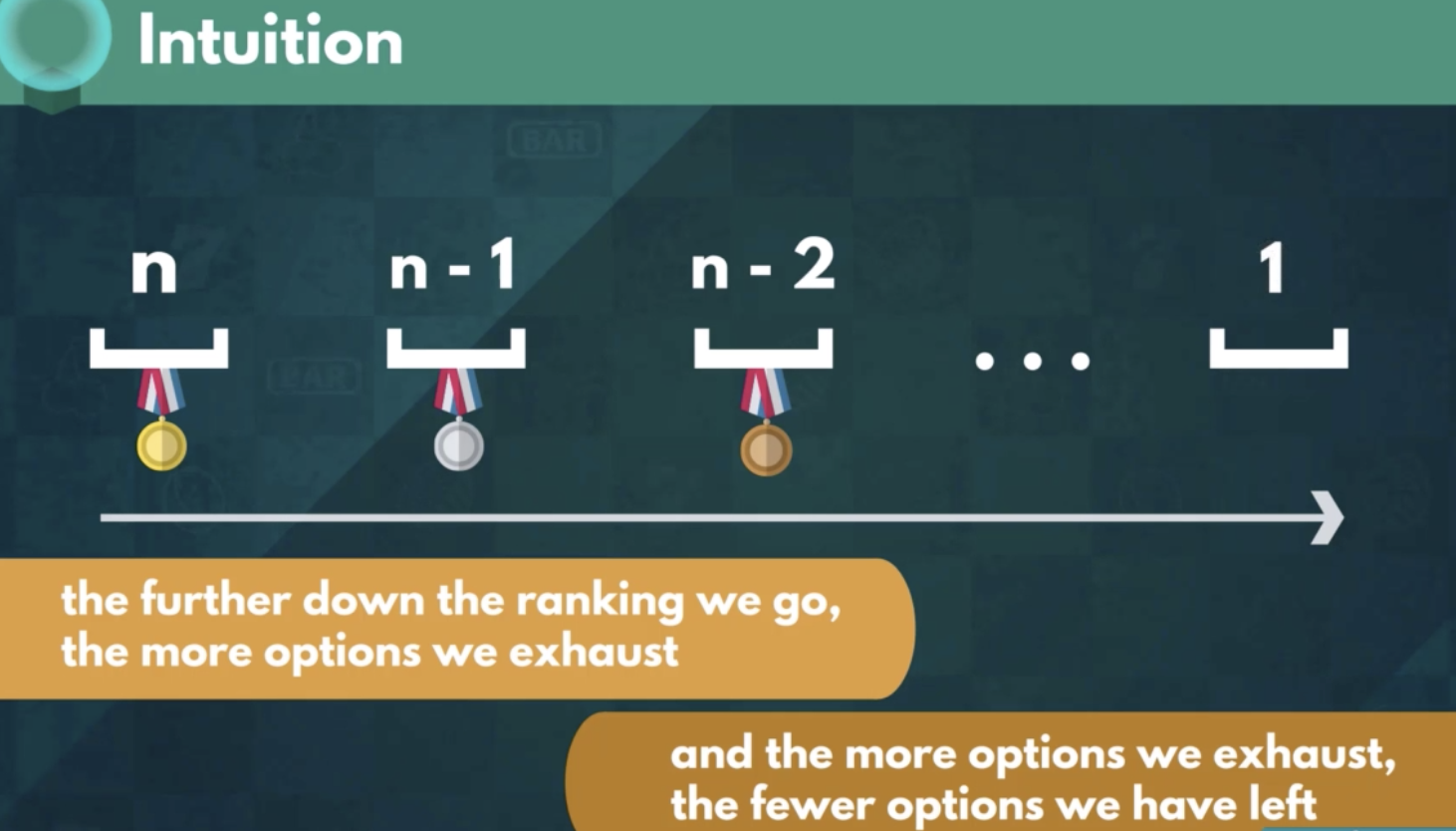
• The number of different possible ways we can arrange a set of elements
• The order is crucial
• You always arrange the entire set of elements in the sample space

$$P_{n}=n\times (n-1)\times (n-2)\times \cdots \times 1=n!$$

2.2 Factorial

$$n!=1\times 2\times 3\times \cdots \times n$$

The product of the natural numbers from 1 to n

2.2.1 Properties

• Negative numbers don't have a factorial
• $0!=1$
• $(n+k)!$ & $(n-k)!$

$$(n+k)!=n!\times (n+1)\times (n+2)\times \cdots \times (n+k)$$

$$(n-k)!=\frac{n!}{(n-k+1)\times (n-k+2)\times \cdots \times (n-k+k)}\\=\frac{n!}{(n-k+1)\times (n-k+2)\times \cdots \times (n)}$$

• Two factorials $n> k$

$$\frac{n!}{k!}=(k+1)\times (k+2)\times \cdots \times n$$

2.3 Variations

2.3.1 Variation with repetition

• The total number of ways we can pick and arrange some elements of a given set
• The order is crucial

2.3.2 Variation without repetition

2.4 Combination

• The number of different ways we can pick certain elements of a set
• Variations don't take into account double counting elements
• All the different permutations of a single combination are different variations

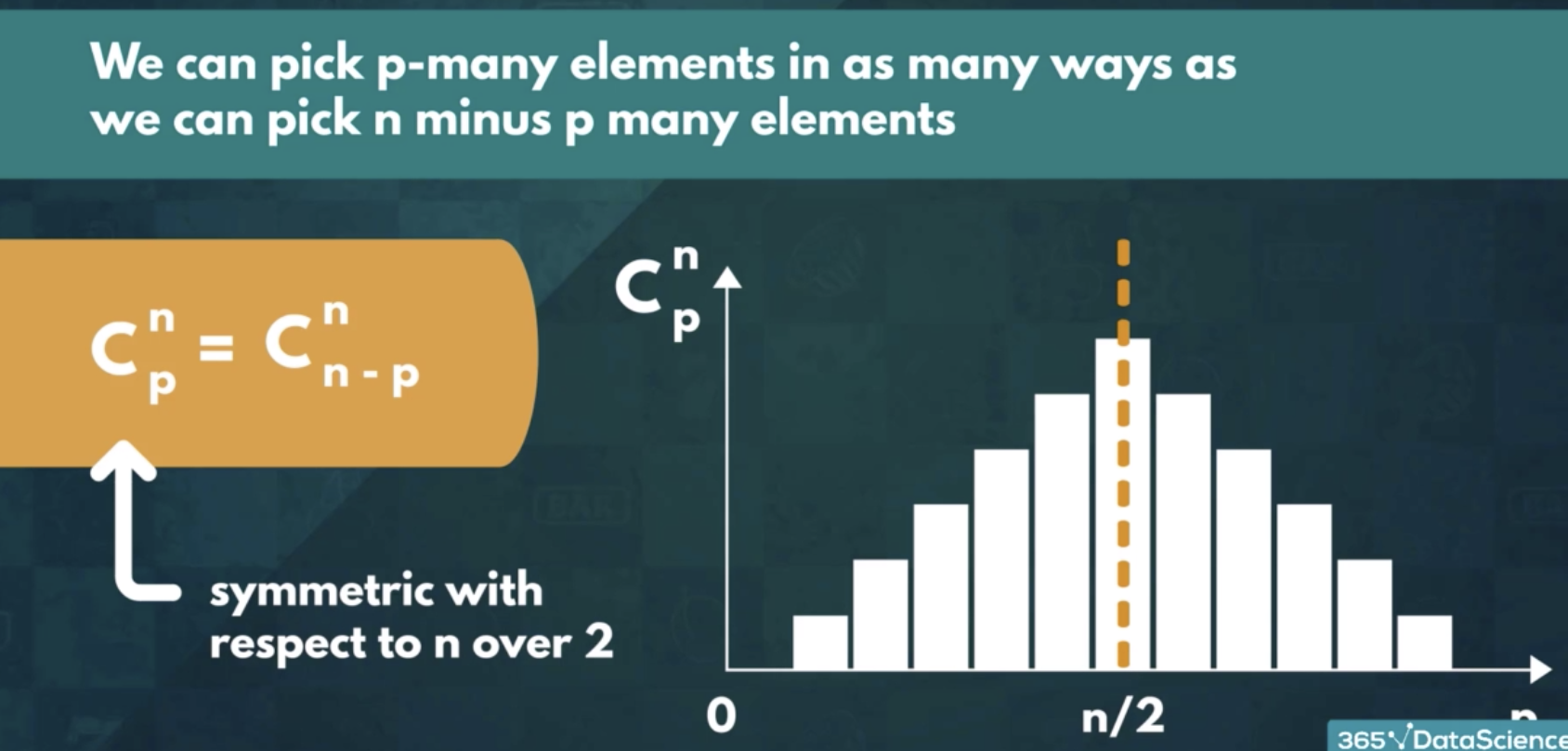
2.4.1 Symmetry of combination

Prerequisite: $p> \frac{n}{2}> n-p$

We can pick p-many elements in as many ways as we can pick n minus p many elements

Apply symmetry to avoid calculating factorials of large numbers to simplify calculations

2.4.2 Combine combinations of events with seperate sample spaces

Calculating the total number of combination is by multiplying the number of options available for each individual event

2.5 Independent events

The likelihood of two independent events occuring simultaneously equals the product of their individual probabilities

3. Example

3.1 Permutation

3.2 Factorials

3.3 Variation without repetition

3.4 Combination

3.5 Symmetry of combination

3.6 Combine combinations of events with seperate sample spaces

3.7 Lottery

4. Summary

4.1 No repetition

4.2 Repetition

5. Reference

https://365datascience.co

https://en.wikipedia.org/wiki/Combinatorics