Set

1. Overview

Bayesian inference is a method of statistical inference in which Bayes' theorem is used to update the probability for a hypothesis as more evidence or information becomes available. Bayesian inference is an important technique in statistics, and especially in mathematical statistics. Bayesian updating is particularly important in the dynamic analysis of a sequnce of data. Bayesian inference has found application in a wide range of activities, including science, engineering, philosophy, medicine, sports, and law. In the philosophy of decision theory, Bayesian inference is closely related to subjective probability, often called "Bayesian probability".

2. Description

2.1 Event and Set

 

2.1.1 Notation

$$x\in A$$

element x included in A

$$x\notin A$$

element x not included in A

$$\forall x\in A$$
For all x in A

$$\forall x\in A:\: x\: is\: even$$
For all x in A, such that, x is even

$$A\subseteq  B$$

Every element of A is also an element of B

2.1.1 Property

• Set: Any set can be either empty or have values in it

The empty set = The null set

Non-empty set = Finite or Infinite

• Subset: 

$$A \subseteq  A$$

$$\varnothing \subseteq  A$$

2.1.2 Convention

Set: Upper case

Element: Lower case

3. Intersection

$$A\cap B$$

All the outcomes that are favourable for both event A and event B simultaneously

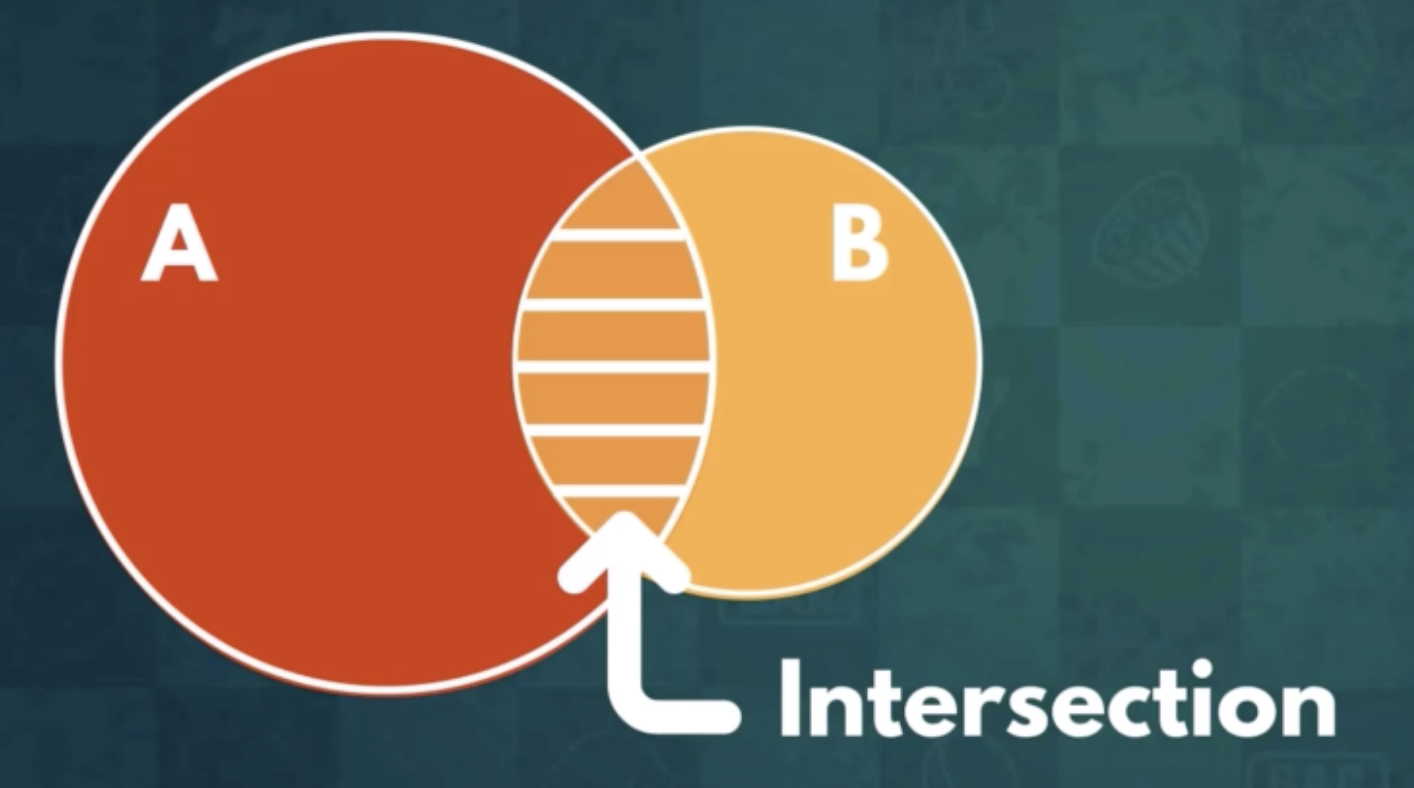
3.1 Cases

3.1.1 Case 1

3.1.2 Case 2

3.1.3 Case 3

 

4. Union

$$A\cup B$$

A combination of all outcomes preferred for either A or B

4.1 Cases

4.1.1 Case 1

4.1.2 Case 2

$$A\cup B=A+B-A\cap B$$

Universally true, regardless of the relationship between A and B

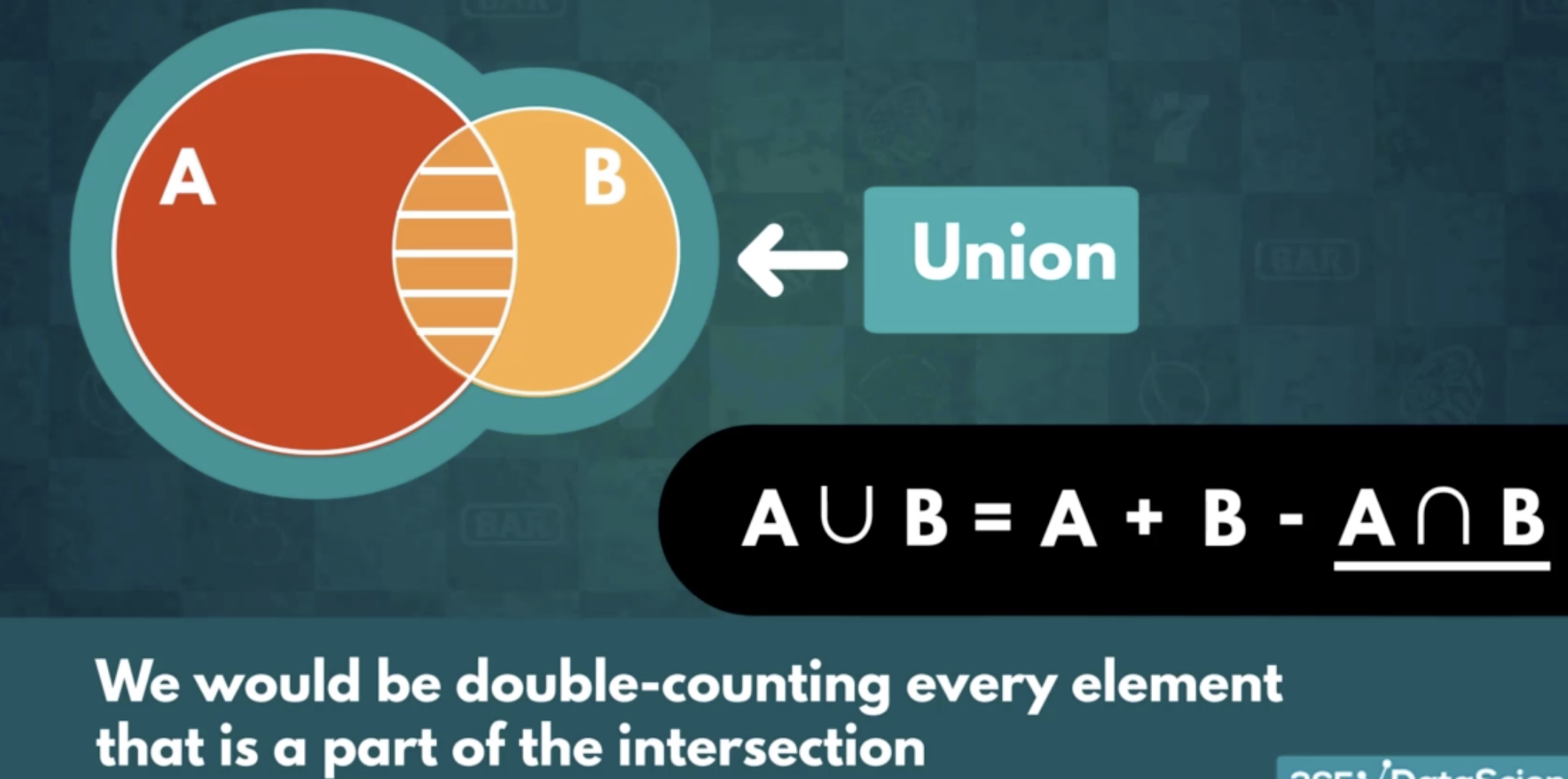
4.1.3 Case 3

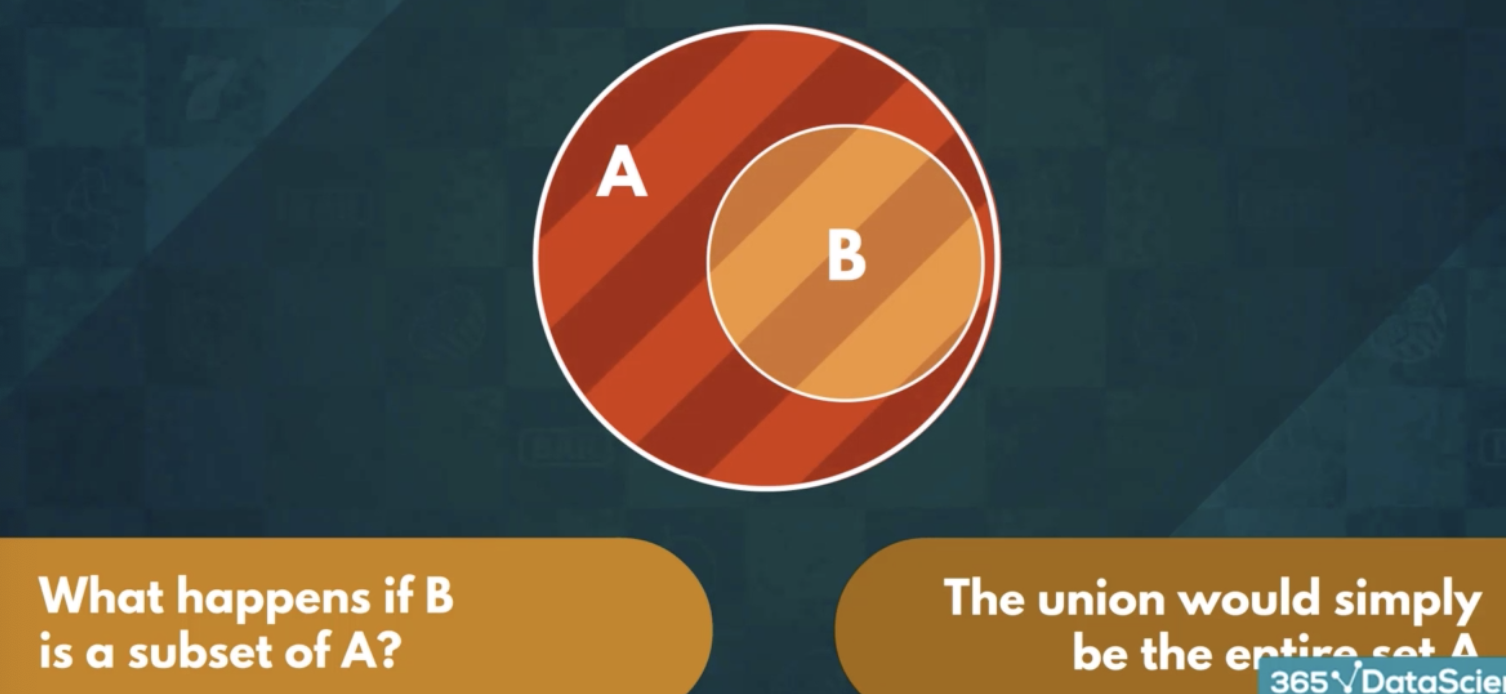
5. Mutually exclusive

$$A\cup B=A+B$$

• Sets, which are not allowed to have any overlapping elements
• Mutually exclusive sets have the empty set as their intersection
• If the intersection of any number of sets is the empty set, then they must be mutually exclusive

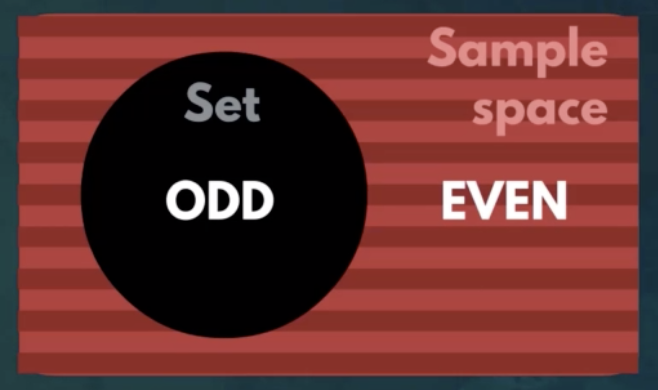
6. Complement set

• All values that are part of the sample space, but not part of the set
• Complements are always mutually exclusive
• Not all mutually exclusive sets are complements

4. Example

4.1 intersection

4.1.1 Example 1

4.1.2 Example 2

4.1.3 Example 3

4.2 Union

4.2.1 Example 1

4.2.2. Example 2

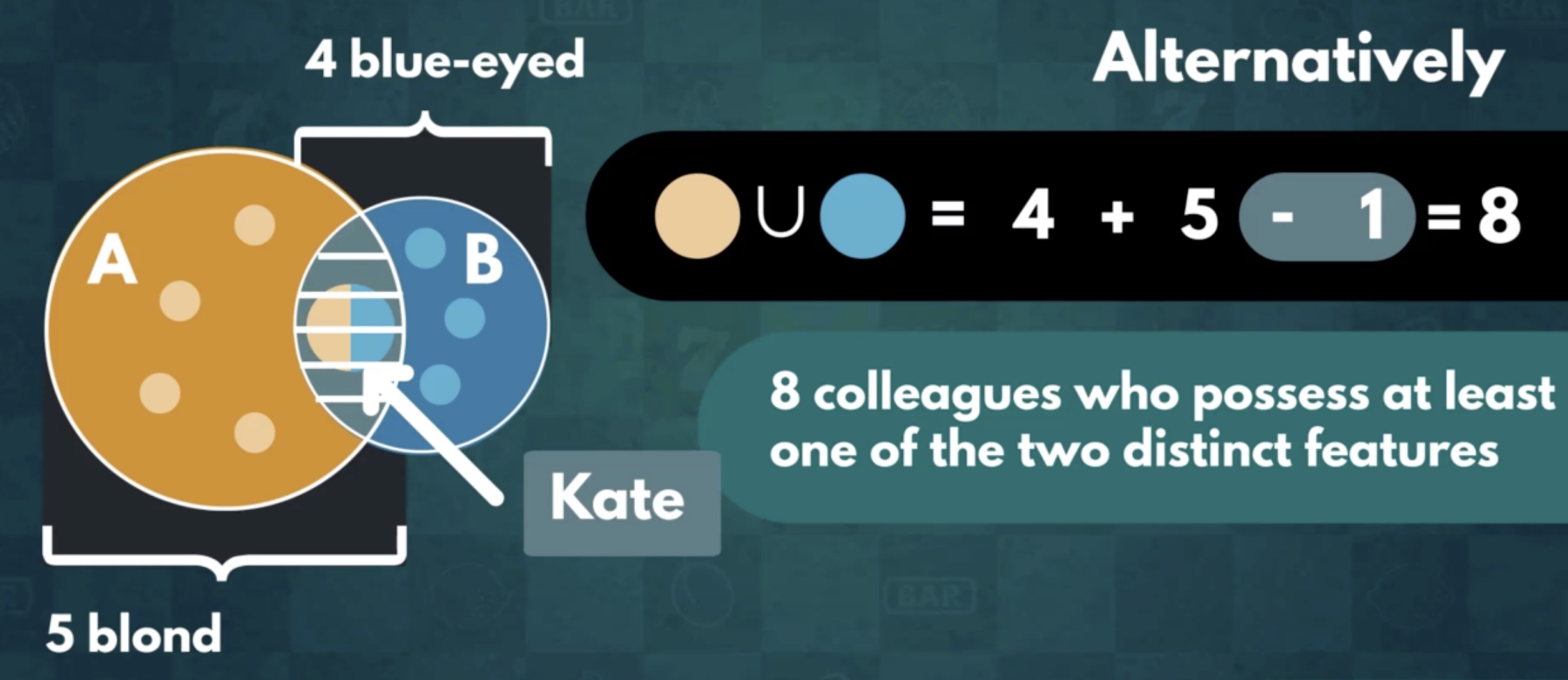
4.2.3 Example 3

4.3 Complement

5. Reference

https://365datascience.co

https://en.wikipedia.org/wiki/Set_(mathematics)