Error Metrics

1. Overview

An Error Metric is a type of Metric used to measure the error of a forecasting model. They can provide a way for forecasters to quantitatively compare the performance of competing models. These are also called loss functions. 

2. Description

2.1 Error (Residual Error)

$$Error=y-\hat{y}$$

Where actual values are denoted by y. Predicted values are denoted by $\hat{y}$

Ideal condition (hypothetical one) is that this error (difference) is 0, which means our model can predict all values correctly (which is not going to happen). Our primary objective is to keep these predicted values closer to actual values.

2.1 Mean absolute error (MAE)

$$MAE=\frac{\sum_{i=1}^{n}\left | y_{i}-\hat{y}_{1} \right |}{n}$$

MAE is the sum of absolute differences between actual and predicted values. It doesn’t consider the direction, that is, positive or negative. When we consider directions also, that is called Mean Bias Error (MBE), which is a sum of errors(difference).  

2.2 Sum Squared Error (SSE)

$$SSE=\sum_{i=1}^{n}(y_{i}-\hat{y}_{i})^{2}$$

To find the Sum Squared Error, we first take the difference between the true and predicted value and we square it and after summing them all up we get Sum Squared Error.

2.3 Mean squared error

$$MSE=\frac{1}{n}\sum_{i=1}^{n}(y_{i}-\hat{y})^{2}$$

Mean square error is always positive and a value closer to 0 or lower value is better. Let’s see how this is calculated

2.4 Root Mean Square Error (RMSE)

$$RMSE=\sqrt{\frac{1}{n}\sum_{i=1}^{n}(y_{i}-\hat{y})^{2}}$$

RMSE is a popular formula to measure the error rate of a model. It is the standard deviation of the error (residual error). However, it can only be compared between models whose errors are measured in the same units. Square root of MSE yields root mean square error (RMSE). So it’s formula is quite similar to what you have seen with mean square error, it’s just that we need to add a square root sign to it. The effect of each error on RMSE is directly proportional to the squared error therefore, RMSE is sensitive to outliers and can exaggerate results if there are outliers in the data set.

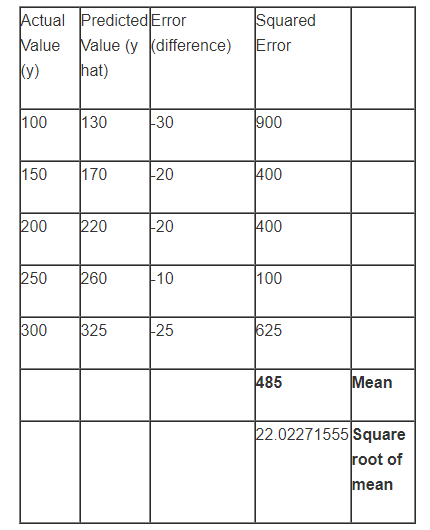
2.5 Root mean squared log error (RMSLE)

 

2.6 Relative Squared Error (RSE)

$$RSE=\frac{\sum_{i=1}^{n}(y_{i}-\hat{y}_{i})^{2}}{\sum_{i=1}^{n}(z_{i}-\hat{z}_{i})^{2}}$$

It can be used to compare between models whose errors are measured in different units.  We can use this method to solve one drawback of MSE which is its sensitivity to the mean and scale of predictions. Here we divide the MSE of our model with the MSE of a model which uses the mean as the predictor i.e. the line of best fit is simply the mean of the Y variable. This provides us with an output which is a ratio where if the output is bigger than 1 then this indicates that the model created by us is not even as good as a model which simply predicts the mean as the prediction for each observation.

2.7 Coefficient of Determination ($R^{2}$)

$$R^{2}=\frac{SSR}{SST}$$

It is a relative measure and takes values ranging from 0 to 1. and R squared of 0 means your regression line explains none of the variability of the data. And, R-squared of 1 would mean your model explains the entire variability of the data. 

The R squared measures the goodness of fit of your model to your data. The more factors you include in your regression the higher the $R^{2}$

2.8 Adjusted $R^{2}$

2.3 AUC

2.4 Lift

2.5 F1 Score

2.6 Generalized least squares

2.7 Maximum likelihood estimation

2.8 Bayesian regression

2.9 Kernel regression

2.10 Gaussian process regression

3. Reference

https://www.saedsayad.com/model_evaluation_r.htm

https://en.wikipedia.org/wiki/Error_metric

https://www.youtube.com/watch?v=K490SP-_H0U

https://www.youtube.com/watch?v=c68JLu1Nfkw

https://en.wikipedia.org/wiki/Error_metric

https://www.youtube.com/watch?v=sHOBQbeSAb0

https://akhilendra.com/evaluation-metrics-regression-mae-mse-rmse-rmsle/

https://www.datavedas.com/model-evaluation-regression-models/