Stack

AlgoDS/DataStructure 2020. 1. 16. 23:04

1. Overview

Stack is a linear data structure that follows a particular order in which the operations are performed. The order may be LIFO(Last In First Out) or FILO(First In Last Out).

2. Description

2.1 Operations

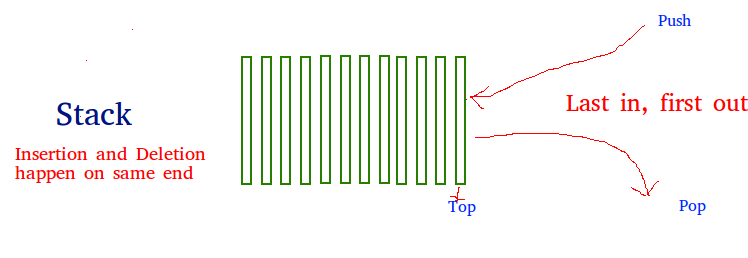
2.1.1 Push

Adds an item in the stack. If the stack is full, then it is said to be an Overflow condition.

2.1.2 Pop

Removes an item from the stack. The items are popped in the reversed order in which they are pushed. If the stack is empty, then it is said to be an Underflow condition.

2.1.3 Peek or Top

Returns the top element of the stack.

2.1.4 isEmpty

Returns true if the stack is empty, else false.

2.2 Time and Space Complexity

Algorithm	Worst
Space	O(n)
Search	O(1)
Insert	O(1)
Delete	O(1)

2.3 Application

Balancing of symbols
Infix to Postfix / Prefix conversion
Redo-undo features at many places like editors, photoshop.
Forward and backward feature in web browsers
Used in many algorithms like Tower of Hanoi, tree traversals, stock span problem, histogram problem.
Other applications can be Backtracking, Knight tour problem, a rat in a maze, N queen problem, and sudoku solve
In Graph Algorithms like Topological Sorting and Strongly Connected Components

2.4 Implementation

# Python program for implementation of stack 
  
# import maxsize from sys module  
# Used to return -infinite when stack is empty 
from sys import maxsize 
  
# Function to create a stack. It initializes size of stack as 0 
def createStack(): 
    stack = [] 
    return stack 
  
# Stack is empty when stack size is 0 
def isEmpty(stack): 
    return len(stack) == 0
  
# Function to add an item to stack. It increases size by 1 
def push(stack, item): 
    stack.append(item) 
    print(item + " pushed to stack ") 
      
# Function to remove an item from stack. It decreases size by 1 
def pop(stack): 
    if (isEmpty(stack)): 
        return str(-maxsize -1) # return minus infinite 
      
    return stack.pop() 
  
# Function to return the top from stack without removing it 
def peek(stack): 
    if (isEmpty(stack)): 
        return str(-maxsize -1) # return minus infinite 
    return stack[len(stack) - 1] 
  
# Driver program to test above functions     
stack = createStack() 
push(stack, str(10)) 
push(stack, str(20)) 
push(stack, str(30)) 
print(pop(stack) + " popped from stack")