-
Activation FunctionsMLAI/DeepLearning 2020. 1. 30. 14:32
1. Overview
In artificial neural networks, the activation function of a node defines the output of that node given an input or set of inputs. A standard computer chip circuit can be seen as a digital network of activation functions that can be "ON" (1) or "OFF" (0), depending on the input. This is similar to the behavior of the linear perceptron in neural networks. However, only nonlinear activation functions allow such networks to compute nontrivial problems using only a small number of nodes.
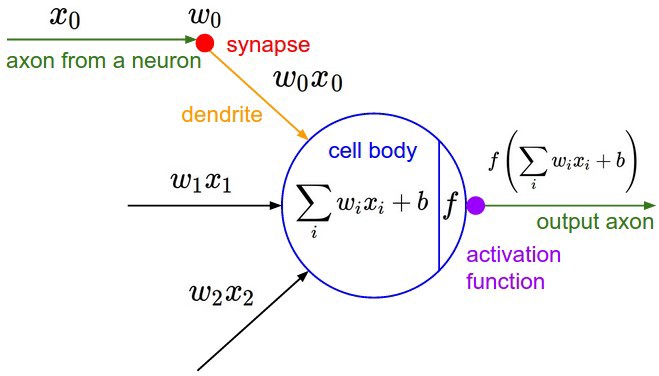
2. Description
2.1 Motivation
$$Y=\sum(weight\times input)+bias$$
The value of Y can be anything ranging from -inf to +inf. The neuron really doesn’t know the bounds of the value. So how do we decide whether the neuron should fire or not ( why this firing pattern? Because we learned it from biology that’s the way the brain works and the brain is a working testimony of an awesome and intelligent system ).
We decided to add “activation functions” for this purpose. To check the Y value produced by a neuron and decide whether outside connections should consider this neuron as “fired” or not. Or rather let’s say — “activated” or not.
2.1.1 Vanishing Gradient Problem
As the backpropagation method progresses downwards (or backward) from the output layer to the input layer, the gradient frequently becomes less and smaller until they approach 0, leaving the weights of the beginning or lower layers essentially unchanged. As a result, gradient descent never converges to the best solution. This is known as the problem of vanishing gradient.

Vanishing gradients are common when the Sigmoid or Tanh activation functions are used in the hidden layer units. When the inputs grow extremely small or extremely large, the sigmoid function saturates at 0 and 1 while the tanh function saturates at -1 and 1.
In both of these examples, the derivatives are very near to 0. Let's name these function ranges/regions saturated regions or terrible regions. As a result, if your input is located in one of the saturating regions, it has essentially no gradient to propagate back through the network.
2.1.2 Exploding Gradient Problem
The direction and magnitude of an error gradient are calculated during the training of a neural network and are used to update the network weights in the correct direction and by the appropriate amount.

Error gradients can collect during an update in deep networks or recurrent neural networks, resulting in very high gradients. As a result, the network weights are updated often, resulting in an unstable network. Weight values can become so large that they overflow and result in NaN values if taken to an extreme. The explosion is caused by continually multiplying gradients through network layers with values greater than 1.0, resulting in exponential growth.
Exploding gradients in deep multiplayer Perceptron networks can lead to an unstable network that can't learn from the training data at best and can't update the weight values at worst. Exploding gradients in recurrent neural networks can result in an unstable network that can't learn from training data and, at best, can't learn over long input sequences of data.
2.1.3 Issues of vanishing and exploding gradient
Certain activation functions, such as the logistic function (sigmoid), have a relatively large difference in variance between their inputs and outputs. To put it another way, they reduce and transform a bigger input space into a smaller output space that sits between 0 and 1.
Similarly, suppose that the initial weights supplied to the network result in a high loss in some circumstances. Gradients can now collect during an update, resulting in very big gradients, which eventually results in huge modifications to network weights, resulting in an unstable network. The parameters can occasionally become so enormous that they overflow and produce NaN values.
2.1.4 ReLu can solve the vanishing gradient problem
The sigmoid activation function is prone to disappearing gradients, especially when several of them are coupled
together. This is because the sigmoid function saturates at 0 for large negative values and at one for positive values.

As you may be aware, rather than the logistic sigmoid function, most neural network topologies now use the rectified linear unit (ReLU) as an activation function in the hidden layers. If the input value is positive, the ReLU function returns it. If it is negative, it returns 0.
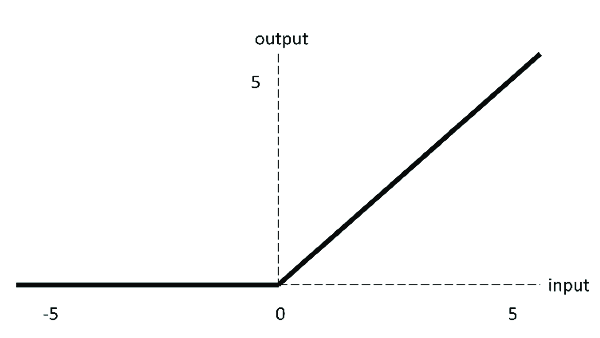
The negative component of the ReLU function cannot be discriminated against because it is 0. As a result, negative values’ derivatives are simply set to 0.
2.1.5 ReLU can cause Exploding Gradient Problem
The sigmoid and Tanh activation functions were used as the default activation function for a long time. For modern deep learning neural networks, the rectified linear activation function is the default activation function. The ReLU can be used with almost any kind of neural network. It is suggested that Multilayer Perceptron (MLP) and Convolutional Neural Network (CNN) models make it the default (CNNs). The use of ReLU with CNNs has been extensively researched and almost always results in improved results, which may surprise you at first.
When combined with CNNs, ReLU can be used as the activation function on the filter maps, followed by a pooling layer. LSTMs have traditionally used the Tanh activation function to activate the cell state and the sigmoid activation function to activate the node output. ReLU was thought to be unsuitable for Recurrent Neural Networks (RNNs) such as the Long Short-Term Memory Network (LSTM) by default due to their careful design.
ReLU is an activation function that is well-known for mitigating the vanishing gradient problem, but it also makes it simple to generate exploding gradients if the weights are large enough, which is why weights must be initialized to very small values. The exploding gradient is the inverse of the vanishing gradient and occurs when large error gradients accumulate, resulting in extremely large updates to neural network model weights during training. As a result, the model is unstable and incapable of learning from your training data.
Although using He initialization in combination with any variant of the Relu activation function can significantly reduce the problem of vanishing/exploding gradients at the start of the training, it does not guarantee that they will not reappear later.
The bias on the node is the input with a fixed value. The bias has the effect of altering the activation function, and the bias input value is traditionally set to 1.0. Consider setting the bias to a low value, such as 0.1, when utilizing ReLU in your network. The weights of a neural network must be initialized to small random values before training. When you use ReLU in your network and set the weights to small random values centered on 0, half of the units will output a 0 value by default.
For example, following uniform weight initialization, almost half of the continuous output values of hidden units are genuine zeros. The output of ReLU is unbounded in the positive domain by design. This means that the output can, in some situations, continue to grow in size. In this situation, if high error gradients develop in the network due to potential error, this causes the size weights to grow, causing the model to behave unstably or improperly.
To prevent this, we must employ certain regularization approaches, such as an L1 or L2 vector norm. This is an excellent approach for promoting sparse representations (e.g., with L1 regularization) and lowering the model’s generalization error.
2.1.6 Nonlinearity
Artificial neural networks are designed as universal function approximators and are intended to work on this target. This means that they must have the ability to calculate and learn not only linear but any function. Thanks to the non-linear activation functions, stronger learning of networks can be achieved.
If we do not have the activation function the weights and bias would simply do a linear transformation. A linear equation is simple to solve but is limited in its capacity to solve complex problems and has less power to learn complex functional mappings from data. A neural network without an activation function is just a linear regression model.
They allow “stacking” of multiple layers of neurons to create a deep neural network. Multiple hidden layers of neurons are needed to learn complex data sets with high levels of accuracy.
2.1.7 Why derivative/differentiation is used?
- Allow back-propagation
When updating the curve in the backpropagation optimization strategy, to know in which direction and how much to change or update the curve depending upon the slope.
3. Types
3.1 Identity

3.1.1 Equation
$$f(x)=x$$
3.1.2 Derivative(with respect to x)
$${f}'(x)=1$$
3.1.3 Pros
- Easy
3.1.4 Cons
- Back-propagation is impossible
- No relation to the input X because the derivative of the function is constant.
- Impossible to go back and understand which weights in the input neurons can provide a better prediction
- All layers of the neural network collapse into one
- with linear activation functions, no matter how many layers in the neural network, the last layer will be a linear function of the first layer
- Output a linear function of input
- No matter how many layers our neural network has, it will still behave just like a single-layer network because summing these layers will give us another linear function that is not strong enough to model data.
3.2 Binary step(Step function, Threshold function)

3.2.1 Equation
$$f(x)=\left\{\begin{matrix}
0\: for\: x< 0\\
1\: for\: x\geq 0
\end{matrix}\right.$$3.2.2 Derivative
$${f}'(x)=\left\{\begin{matrix}
0\: for\, x\neq 0\\
?\: for\, x= 0
\end{matrix}\right.$$3.2.3 Pros
- If the input value is above or below a certain threshold, sending exactly the same signal to the next layer
3.2.4 Cons
- Not allow multi-value outputs
- It cannot support classifying the inputs into one of several categories
3.3 Sigmoid function(Logistic, Soft step)

3.3.1 Equation
$$f(x)=\sigma (x)=\frac{1}{1+e^{-x}}$$
3.3.2 Derivative
$${f}'(x)=f(x)(1-f(x))$$
3.3.3 Pros
- Easy to understand and apply it
- Smooth gradient, preventing jumps in output values
- Output values bound between 0 and 1, normalizing the output of each neuron
- Clear predictions
- For X above 2 or below -2, it tends to bring the Y value (the prediction) to the edge of the curve, very close to 1 or 0. This enables clear predictions.
3.3.4 Cons
- Vanishing and Exploding gradients

The local gradient is really small. It will make slowly vanish close to no signal flow through neurons to its weight. This can result in the network refusing to learn further, or being too slow to reach an accurate prediction.
- The output isn't Zero-centered
This makes gradient of weights either all positives or all negatives. It makes the gradient updates go too far in different directions. 0 < output < 1, and it makes optimization harder.
- Slow convergence
- Sigmoids saturate and kill gradients
- Computationally expensive
3.4 Hyperbolic Tangent function (Tanh)

3.4.1 Equation
$$f(x)=tanh(x)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}$$
3.4.2 Derivative
$${f}'(x)=1-f(x)^{2}$$
3.4.3 Pros
- The output is zero-centered because its range in between -1 to 1.
- Easier optimization. It is always preferred over Sigmoid function
- Otherwise like the Sigmoid function
3.4.4 Cons
- Vanishing gradient problem
- Otherwise like the Sigmoid function
3.5 Rectified Linear unit(ReLU)

3.5.1 Equation
$$f(x)=\left\{\begin{matrix}
0\: for\: x\leq 0\\
x\: for\: x>0
\end{matrix}\right.$$3.5.2 Derivative
$${f}'(x)=\left\{\begin{matrix}
0\: for\: x\leq 0\\
1\: for\: x>0
\end{matrix}\right.$$3.5.3 Pros
- Computationally Efficient
- Non-linear
- Although it looks like a linear function, ReLU has a derivative function and allows for backpropagation
- Avoids and rectifies the vanishing gradient problem
3.5.4 Cons
- Only be used within Hidden layers of a Neural Network Model
- Should use a Softmax function for a Classification problem
- Should use a linear function for a regression problem
- The Dying ReLU problem
- Some gradient can be fragile during training and can die
- To fix this problem Using Leaky ReLu
3.6 Leaky ReLU

3.6.1 Equation
$$f(x)=\left\{\begin{matrix}
0.01x\: for\: x<0\\
x\: for\: x\geq 0
\end{matrix}\right.$$3.6.2 Derivative
$${f}'(x)=\left\{\begin{matrix}
0.01\: for\: x<0\\
1\: for\: x\geq 0
\end{matrix}\right.$$3.6.3 Pros
- Prevent dying ReLU problem
- This variation of ReLU has a small positive slope in the negative area, so it does enable backpropagation, even for negative input values
- Otherwise like ReLU
3.6.4 Cons
- Results not consistent
- Leaky ReLU does not provide consistent predictions for negative input values.
3.7 Softmax function
4. Which activation function should be preferred?
Answer to this question is that nowadays we should use ReLu which should only be applied to the hidden layers. And if your model suffers from dead neurons during training we should use leaky ReLu or Maxout function.
It’s just that Sigmoid and Tanh should not be used nowadays due to the vanishing Gradient Problem which causes a lot of problems to train, degrades the accuracy and performance of a Deep Neural Network Model.
5. Example
6. Reference
https://en.wikipedia.org/wiki/Activation_function
https://www.youtube.com/watch?v=9vB5nzrL4hY
https://www.youtube.com/watch?v=-7scQpJT7uo
https://towardsdatascience.com/complete-guide-of-activation-functions-34076e95d044
https://towardsdatascience.com/activation-functions-and-its-types-which-is-better-a9a5310cc8f
https://medium.com/@snaily16/what-why-and-which-activation-functions-b2bf748c0441
https://dashee87.github.io/deep%20learning/visualising-activation-functions-in-neural-networks/
'MLAI > DeepLearning' 카테고리의 다른 글
Sigmoid and Softmax (0) 2022.07.07 Boltzmann Machine with Energy-Based Models and Restricted Boltzmann machines(RBM) (0) 2019.10.19 Classify Deep Learning (0) 2019.10.16 Softmax and Cross-Entropy with CNN (0) 2019.10.16 Artificial neural network(ANN) (0) 2019.10.05