Sigmoid and Softmax

1. Softmax

Softmax function calculates the probability distribution of the event over k different events. This function will calculate the probabilities of each target class over all possible target classes.

Equation

$$P(y=j | x) = \frac{e^{x_j}}{\sum_{k=1}^K e^{x_k}}$$

Plot

x = np.arange(-2.0, 6.0, 0.1)
input = np.vstack([x, np.ones_like(x), 0.2 * np.ones_like(x)])

input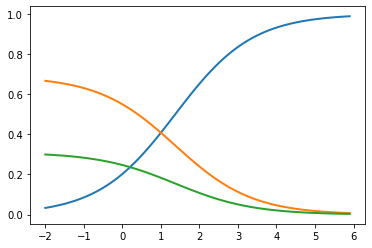

Characteristic

1. It normalizes your data: Outputs a proper probability distribution
2. It is differentiable
   1. A hardmax function such as argmax is not differentiable. The softmax gives at least a minimal amount of probability to all elements in the output vector, and so is nicely differentiable, hence the term “soft” in softmax
3. It uses the exponential form. The interesting property of the exponential function combined with the normalization in the softmax is that high scores in x become much more probable than low scores

2. Sigmoid

Equation

$$sigmoid(x_{i})=\sigma(x)=\frac{1}{1+e^{-x_{i}}}$$

Plot

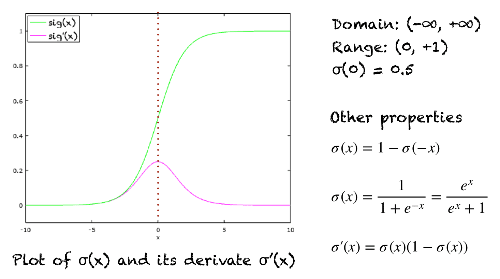
Characteristic

Input domain: $(-\infty, +\infty )$

Output range: (0, +1)

$\sigma(0)=0.5$

The function is monotonically increasing

The function is continuous everywhere

The function is differentiable everywhere in its domain

Numerically, it is enough to compute this function’s value over a small range of numbers, e.g., [-10, +10]. For values less than -10, the function’s value is almost zero. For values greater than 10, the function’s values are almost one

Reference

https://datascience.stackexchange.com/questions/23159/in-softmax-classifier-why-use-exp-function-to-do-normalization

https://www.quora.com/How-does-softmax-relate-to-the-true-probability-of-a-sample-being-correctly-classified

https://machinelearningmastery.com/a-gentle-introduction-to-sigmoid-function/