Gauss Elimination and Gauss-Jordan Elimination

1. Overview

Row reduction is the process of performing row operations to transform any matrix into (reduced) row echelon form. In reduced row echelon form, each successive row of the matrix has less dependencies than the previous, so solving systems of equations is a much easier task. The idea behind row reduction is to convert the matrix into an "equivalent" version in order to simplify certain matrix computations. Its two main purposes are to solve system of linear equations and calculate the inverse of a matrix.

• Gaussian elimination: Uses row operations to produce a row-echelon matrix
• Gaussian-Jordan elimination: Uses row operations to produce a reduced row-echelon matrix

 

2. Description

2.1 Invertibility

Only square matrices can be invertible, because reversal is commutative $AA^{-1}=A^{-1}A=1$. But not all square matrices have inverses. The determinant of a matrix checks for invertibility. $Det(A)\neq 0$ iff A is invertible

 

• $AX=B\rightarrow $ multiply both sides by $A^{-1}$ on the right $\rightarrow X=A^{-1}B$
• $XA=B\rightarrow $ multiply both sides by $A^{-1}$ on the right $\rightarrow X=BA^{-1}$
• $ABXC=E\rightarrow $ put $C^{-1}$ on the right and $B^{-1}A^{-1}$ on the left $\rightarrow X=B^{-1}A^{-1}EC^{-1}$

 

2.2 Gauss Jordan Elimination

To solve $Ax=b$, we must find inverse matrix $A^{-1}$. This can be done via Gauss-Jordan Elimination. this method affords three row operations:

• Linear Combination: $R_{i}$ += $kR_{j}$
• Scaling $R_{i}$ *= k
• Row Swap: $R_{i}\leftrightharpoons R_{j}$

After creating a matrix of the form $Ax=b$, we can solve for x be creating an augmented matrix of the for $\left [ A\: |\: b \right ]$, and converting the left-hand side into the identity matrix:

To solve for x algebraically, $Ax=b\rightarrow A^{-1}Ax=A^{-1}b\rightarrow 1x=A^{-1}b$. So Gauss-Jordan facilitates the discovery of inverse matrix $A^{-1}$. We can show this computation explicitly, by setting an augmented matrix of form $\left [ A\: |\: 1 \right ]$

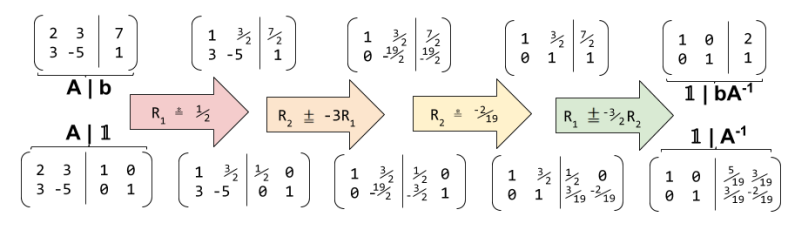
Row operations are functions that act on vectors. So are matrices.

3. References

https://brilliant.org/wiki/gaussian-elimination/

https://en.wikipedia.org/wiki/Gaussian_elimination

https://en.wikipedia.org/wiki/Row_echelon_form

https://en.wikipedia.org/wiki/System_of_linear_equations

https://en.wikipedia.org/wiki/Rank_(linear_algebra)

https://en.wikipedia.org/wiki/Determinant

https://en.wikipedia.org/wiki/Elementary_matrix#Operations

https://en.wikipedia.org/wiki/Invertible_matrix

https://slideplayer.com/slide/8898171/